Raíz cúbica

De Wikipedia, la enciclopedia libre

Saltar a: navegación, búsqueda

Representación gráfica de la función: y = ${\displaystyle {\sqrt[{3}]{x}}}$

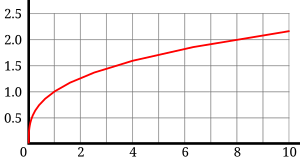
La raíz cúbica, en el sistema de los números reales, estrictamente es la función inversa de la función ${\displaystyle y=x^{3}}$. La extracción de la raíz cúbica de cualquier número real puede admitirse como una operación unaria de los reales en los reales. ^{[1] [2]}
La operación de calcular la raíz cúbica se puede efectuar sin restricciones en el cuerpo de los números reales, obviamente con aproximaciones en la mayoría de los casos. Es asociativa con la potenciación y distributiva con la multiplicación y división de números reales, pero no es asociativa ni distributiva con la suma o la resta.
Históricamente, el famoso problema de la duplicación del cubo, estudiado por Arquitas de Tarento, plantéo la solución a través de la raíz cúbica de 2. Esta cuestión no se resolvió con la aritmética de los números racionales, tampoco con la construcción geométrica a través de regla y compás.^[3]
Para facilitar el cálculo de la raíz cúbica, se hacía uso de logaritmos y sus propiedades sobre las raíces usando tablas y también mediante la regla de cálculo; En la actualidad, se trabaja con las calculadoras.^[4]

Índice

 [ocultar] 

• 1 Definición formal
  • 1.1 Números reales
  • 1.2 Números complejos
• 2 Métodos numéricos
• 3 Véase también
• 4 Notas y referencias
• 5 Enlaces externos

Definición formal[editar]

Las raíces cúbicas de un número x son números y que satisfacen la ecuación

${\displaystyle y^{3}=x.}$

Números reales[editar]

Si x e y son reales, entonces existe una única solución tal que la ecuación tiene además una única solución, y ésta corresponde a un número real. Si se emplea esta definición, la raíz cúbica de un número negativo es también un número negativo. De esta forma, la raíz cúbica de x es representada igualmente por:

${\displaystyle {\sqrt[{3}]{x}}=x^{1 \over 3}}$

Si x e y son ambos complejos, entonces se puede decir que posee tres soluciones (si x es no nulo) y así x tiene tres raíces cúbicas: una raíz real y dos complejas, en la forma de par conjugado. Este hecho deja interesantes resultados dentro de las matemáticas. Por ejemplo, las raíces cúbicas del número uno son:

${\displaystyle {\sqrt[{3}]{1}}={\begin{cases}\ \ 1\\-{\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i\\-{\frac {1}{2}}-{\frac {\sqrt {3}}{2}}i\end{cases}}}$

Estas dos raíces se relacionan con todas las otras raíces cúbicas de otros números. Si un número es raíz cúbica de un número real las raíces cúbicas pueden ser calculadas multiplicando el número por las raíces de la raíz cúbica de uno.^[5]

Números complejos[editar]

En el cuerpo de los números complejos, la raíz cúbica responde a la solución de la ecuación

${\displaystyle z^{3}-a=0}$

donde a es cualquier número complejo no nulo. El conjunto solución involucra tres valores distintos; si z es un complejo real uno de los valores es número real; los otros dos son complejos, sin ninguna parte nula. ^[6]
Para los números complejos, el valor principal de las raíces cúbicas se define como:

${\displaystyle z^{1 \over 3}=\exp \left({\operatorname {Log} {z} \over 3}\right)}$

Donde Log(z) es la rama principal del logaritmo complejo. Si se escribe z como

${\displaystyle z=r\exp(i\theta )\,}$

Donde r es un número real positivo y ${\displaystyle \theta }$ cae en el rango:

${\displaystyle -\pi <\theta \leq \pi }$,

entonces la raíz cúbica es

${\displaystyle {\sqrt[{3}]{z}}={\sqrt[{3}]{r}}\exp \left({i\theta \over 3}\right)}$.

Esto significa que en coordenadas polares al tomar la raíz cúbica de un número complejo se está tomando la raíz cúbica del radio y el ángulo polar se está dividiendo en tres partes de tal forma que define las tres raíces. Con esta definición, la raíz cúbica de un número negativo es un número complejo, y por ejemplo ${\displaystyle {\sqrt[{3}]{-8}}}$ no será -2, sino ${\displaystyle 1+i{\sqrt {3}}}$. En aquellos programas que aceptan resultados imaginarios (tales como Mathematica), el grafo de la raíz cúbica de x en el plano de los números reales dará como resultados valores negativos de la raíz por igual.

Métodos numéricos[editar]

El método de Newton es un método iterativo que puede ser usado para calcular la raíz cúbica. Para números reales representados mediante coma flotante, este método se reduce al siguiente método iterativo para producir sucesivas mejores aproximaciones de la raíz cúbica de a:

${\displaystyle x_{n+1}={\frac {1}{3}}\left({\frac {a}{x_{n}^{2}}}+2x_{n}\right).}$

El método es simplemente un promedio de tres factores elegidos de tal manera que

${\displaystyle x_{n}\times x_{n}\times {\frac {a}{x_{n}^{2}}}=a}$

en cada iteración.

Véase también[editar]

• Función raíz
• Método de Newton-Raphson
• Radical jerarquizado
• Raíz cuadrada
• Radicación

Notas y referencias[editar]

1. Volver arriba ↑ Sigler. Algebra
2. Volver arriba ↑ Dubreil: "Algebra Moderna"
3. Volver arriba ↑ Rey Pastor. Babini: "Historia de la matemática"
4. Volver arriba ↑ Conte- De Boor: Análisis numérico
5. Volver arriba ↑ Carlos Vega: "Temas de álgebra", Editorial San Marcos, Lima (1990)
6. Volver arriba ↑ Trejo. Variable compleja

Enlaces externos[editar]

Wikilibros

• Wikilibros alberga un libro o manual sobre cálculo de raíces cúbicas.
• Resolución de raíces cúbicas mediante el método de Newton Raphson

Obtenido de «https://es.wikipedia.org/w/index.php?title=Raíz_cúbica&oldid=97401073»

Categorías:

• Álgebra elemental
• Raíces