Integración

De Wikipedia, la enciclopedia libre

Saltar a: navegación, búsqueda

Para otros usos de este término, véase Integración (desambiguación).

«Integral» redirige aquí. Para otras acepciones, véase Integral (desambiguación).

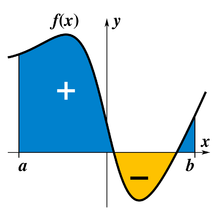
La integral definida de una función representa el área limitada por la gráfica de la función, en un sistema de coordenadas cartesianas con signo positivo cuando la función toma valores positivos y signo negativo cuando toma valores negativos.

La integración es un concepto fundamental del cálculo y del análisis matemático. Básicamente, una integral es una generalización de la suma de infinitos sumandos, infinitamente pequeños.
El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o antiderivación. Es muy común en la ingeniería y en la ciencia también; se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.
Fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de Newton generaron el teorema fundamental del cálculo integral, que propone que la derivación y la integración son procesos inversos.

Índice

 [ocultar] 

• 1 Principales objetivos del cálculo integral
• 2 Teoría
• 3 Historia
  • 3.1 Integración antes del cálculo
  • 3.2 Newton y Leibniz
  • 3.3 Formalización de las integrales
  • 3.4 Notación
  • 3.5 Generalizaciones modernas
• 4 Terminología y notación
• 5 Conceptos y aplicaciones
• 6 Definiciones formales
  • 6.1 Integral de Riemann
  • 6.2 Integral de Darboux
  • 6.3 Integral de Lebesgue
  • 6.4 Otras integrales
• 7 Propiedades de la integración
  • 7.1 Linealidad
  • 7.2 Desigualdades con integrales
  • 7.3 Convenciones
• 8 Teorema fundamental del cálculo
  • 8.1 Enunciado de los teoremas
• 9 Extensiones
  • 9.1 Integrales impropias
  • 9.2 Integración múltiple
  • 9.3 Integrales de línea
  • 9.4 Integrales de superficie
  • 9.5 Integrales de formas diferenciales
• 10 Métodos y aplicaciones
  • 10.1 Cálculo de integrales
  • 10.2 Algoritmos simbólicos
  • 10.3 Cuadratura numérica
• 11 Algunas aplicaciones
  • 11.1 Valor medio de una función
  • 11.2 Aplicaciones en física
• 12 Véase también
• 13 Referencias y notas
• 14 Bibliografía
  • 14.1 Libros en internet
• 15 Enlaces externos

Principales objetivos del cálculo integral[editar]

Sus principales objetivos a estudiar son:

• Área de una región plana
• Cambio de variable
• Integrales indefinidas
• Integrales definidas
• Integrales impropias
• Integral de línea
• Integrales múltiples (dobles o triples)
• Integrales trigonométricas, logarítmicas y exponenciales
• Métodos de integración
• Teorema fundamental del cálculo
• Volumen de un sólido de revolución

Teoría[editar]

${\displaystyle \scriptstyle \ \int _{a}^{b}f(x)\,\mathrm {d} x}$ se interpreta como el área bajo la curva de f, entre a y b.

Dada una función ${\displaystyle f(x)}$ de una variable real ${\displaystyle x}$ y un intervalo ${\displaystyle [a,b]}$ de la recta real, la integral es igual al área de la región del plano ${\displaystyle xy}$ limitada entre la gráfica de ${\displaystyle f}$, el eje ${\displaystyle x}$, y las líneas verticales ${\displaystyle x=a}$ y ${\displaystyle x=b}$, donde son negativas las áreas por debajo del eje ${\displaystyle x}$.

${\displaystyle \int _{a}^{b}f(x)\,{\text{d}}x}$

La palabra "integral" también puede hacer referencia a la noción de primitiva: una función F, cuya derivada es la función dada ${\displaystyle f}$. En este caso se denomina integral indefinida, mientras que las integrales tratadas en este artículo son las integrales definidas. Algunos autores mantienen una distinción entre integrales primitivas e indefinidas.
Los principios de la integración fueron formulados por Newton y Leibniz a finales del siglo XVII. A través del teorema fundamental del cálculo, que desarrollaron los dos de forma independiente, la integración se conecta con la derivación, y la integral definida de una función se puede calcular fácilmente una vez se conoce una antiderivada. Las integrales y las derivadas pasaron a ser herramientas básicas del cálculo, con numerosas aplicaciones en ciencia e ingeniería.
Bernhard Riemann dio una definición rigurosa de la integral. Se basa en un límite que aproxima el área de una región curvilínea a base de partirla en pequeños trozos verticales. A comienzos del siglo XIX, empezaron a aparecer nociones más sofisticadas de la integral, donde se han generalizado los tipos de las funciones y los dominios sobre los cuales se hace la integración. La integral curvilínea se define para funciones vectoriales de una variable, y el intervalo de integración [a,b] se sustituye por el de la parametrización de la curva sobre la cual se está integrando, la cual, conecta dos puntos del plano o del espacio. En una integral de superficie, la curva se sustituye por un trozo de una superficie en el espacio tridimensional.
Las integrales de las formas diferenciales desempeñan un papel fundamental en la geometría diferencial moderna. Estas generalizaciones de la integral surgieron primero a partir de las necesidades de la física, y tienen un papel importante en la formulación de muchas leyes físicas cómo, por ejemplo, las del electromagnetismo. Los conceptos modernos de integración se basan en la teoría matemática abstracta conocida como integral de Lebesgue, que fue desarrollada por Henri Lebesgue.

Historia[editar]

Integración antes del cálculo[editar]

La integración se puede trazar en el pasado hasta el antiguo Egipto, circa 1800 a. C., con el papiro de Moscú, donde se demuestra que ya se conocía una fórmula para calcular el volumen de un tronco piramidal. La primera técnica sistemática documentada capaz de determinar integrales es el método de exhausción de Eudoxo (circa 370 a. C.), que trataba de encontrar áreas y volúmenes a base de partirlos en un número infinito de formas para las cuales se conocieran el área o el volumen. Este método fue desarrollado y usado más adelante por Arquímedes, que lo empleó para calcular áreas de parábolas y una aproximación al área del círculo. Métodos similares fueron desarrollados de forma independiente en China alrededor del siglo III por Liu Hui, que los usó para encontrar el área del círculo. Más tarde, Zu Chongzhi usó este método para encontrar el volumen de una esfera. En el Siddhanta Shiromani, un libro de astronomía del siglo XII del matemático indio Bhaskara II, se encuentran algunas ideas de cálculo integral.
Hasta el siglo XVI no empezaron a aparecer adelantos significativos sobre el método de exhausción. En esta época, por un lado, con el trabajo de Cavalieri con su método de los indivisibles y, por otro lado, con los trabajos de Fermat, se empezó a desarrollar los fundamentos del cálculo moderno. A comienzos del siglo XVII, se produjeron nuevos adelantos con las aportaciones de Barrow y Torricelli, que presentaron los primeros indicios de una conexión entre la integración y la derivación.

Newton y Leibniz[editar]

Los principales adelantos en integración vinieron en el siglo XVII con la formulación del teorema fundamental del cálculo, realizado de manera independiente por Newton y Leibniz. El teorema demuestra una conexión entre la integración y la derivación. Esta conexión, combinada con la facilidad, comparativamente hablando, del cálculo de derivadas, se puede usar para calcular integrales. En particular, el teorema fundamental del cálculo permite resolver una clase más amplia de problemas. También cabe destacar todo el marco estructural alrededor de las matemáticas que desarrollaron también Newton y Leibniz. El llamado cálculo infinitesimal permitió analizar, de forma precisa, funciones con dominios continuos. Posteriormente, este marco ha evolucionado hacia el cálculo moderno, cuya notación para las integrales procede directamente del trabajo de Leibniz.

Formalización de las integrales[editar]

Aunque Newton y Leibniz proporcionaron un enfoque sistemático a la integración, su trabajo carecía de un cierto nivel de rigor. Es memorable la expresión del obispo Berkeley interpretando los infinitesimales como los "fantasmas de las cantidades que se desvanecen".
El cálculo adquirió una posición más firme con el desarrollo de los límites y, en la primera mitad del siglo XIX, recibió una fundamentación adecuada por parte de Cauchy. La integración fue rigurosamente formalizada por primera vez por Riemann, empleando límites. A pesar de que todas las funciones continuas fragmentadas y acotadas son integrables en un intervalo acotado, más tarde se consideraron funciones más generales para las cuales la definición de Riemann no era aplicable y por tanto no eran integrables en el sentido de Riemann. Posteriormente Lebesgue dio una definición diferente de la integral^[1] basada en la teoría de la medida que generalizaba la definición de Riemann, así toda función integrable en el sentido de Riemann también lo es en el sentido de Lebesgue, aunque existen algunas funciones integrables en el sentido de Lebesgue que no lo son en el sentido de Riemann. Más recientemente se han propuesto otras definiciones de integral aún más generales, que amplían las definiciones de Riemann y Lebesgue.

Notación[editar]

El símbolo de integral en escritos (de izquierda a derecha) ingleses, alemanes y rusos.

Isaac Newton usaba una pequeña barra vertical encima de una variable para indicar integración, o ponía la variable dentro de una caja. La barra vertical se confundía fácilmente con ${\displaystyle {\dot {x}}}$ o ${\displaystyle x'\,\!}$, que Newton usaba para indicar la derivación, y además la notación "caja" era difícil de reproducir por los impresores; por ello, estas notaciones no fueron ampliamente adoptadas.
La notación moderna de las integrales indefinidas fue presentada por Gottfried Leibniz en 1675.^{[2] [3]} Para indicar summa (ſumma; en latín, "suma" o "total"), adaptó el símbolo integral, "∫", a partir de una letra S alargada porque consideraba a la integral como una suma infinita de addendas infinitesimales. La notación moderna de la integral definida, con los límites arriba y abajo del signo integral, la usó por primera vez Joseph Fourier en Mémoires de la Academia Francesa, alrededor de 1819–20, reimpresa en su libro de 1822.^{[4] [5]}
Existen ligeras diferencias en la notación del símbolo de la integral en la literatura de las diversas lenguas: el símbolo inglés está inclinado hacia la derecha, en alemán tradicionalmente se ha escrito derecho (sin inclinación) mientras la variante rusa tradicional está inclinada hacia la izquierda.
En la notación matemática en árabe moderno, que se escribe de derecha a izquierda, se usa un signo integral invertido .^[6]

Generalizaciones modernas[editar]

Tras la creación del cálculo integral a partir del siglo XVII, y su desarrollo más o menos intuitivo durante un par de siglos, la noción de integración fue analizada con mayor rigor durante el siglo XIX. Así la primera noción rigurosa de integración es el concepto de integral de Riemann, así como su generalización conocida como integral de Riemann-Stieltjes. A principios del siglo XX, el desarrollo de la teoría de la medida llevó al concepto más general y cualitativamente más avanzado de integral de Lebesgue. Más tarde el desarrollo de la noción de proceso estocástico dentro de la teoría de la probabilidad llevó a la formulación de la integral de Itō hacia el final de la primera mitad del siglo XX, y posteriormente a su generalización conocida como integral de Skorohod (1975). Asimismo desde los años 1960, se ha buscado definición matemáticamente rigurosa de integral de caminos cuánticos.

Terminología y notación[editar]

Si una función tiene una integral, se dice que es integrable. De la función de la cual se calcula la integral se dice que es el integrando. Se denomina dominio de integración a la región sobre la cual se integra la función. Si la integral no tiene un dominio de integración, se considera indefinida (la que tiene dominio se considera definida). En general, el integrando puede ser una función de más de una variable, y el dominio de integración puede ser un área, un volumen, una región de dimensión superior, o incluso un espacio abstracto que no tiene estructura geométrica en ningún sentido usual.
El caso más sencillo, la integral de una función real f de una variable real x sobre el intervalo [a, b], se escribe

${\displaystyle \int _{a}^{b}f(x)\,{\text{d}}x}$

El signo ∫, una "S" alargada, representa la integración; a y b son el límite inferior y el límite superior de la integración y definen el dominio de integración; f es el integrando, que se tiene que evaluar al variar x sobre el intervalo [a,b]; y dx puede tener diferentes interpretaciones dependiendo de la teoría que se emplee. Por ejemplo, puede verse simplemente como una indicación de que x es la variable de integración, como una representación de los pasos en la suma de Riemann, una medida (en la integración de Lebesgue y sus extensiones), un infinitesimal (en análisis no estándar) o como una cantidad matemática independiente: una forma diferencial. Los casos más complicados pueden variar la notación ligeramente.

Conceptos y aplicaciones[editar]

Aproximaciones a la integral de ${\displaystyle {\sqrt {x}}}$ entre 0 y 1, con ■ 5 muestras por la izquierda (arriba) y ■ 12 muestras por la derecha (abajo).

Las integrales aparecen en muchas situaciones prácticas. Considérese una piscina. Si es rectangular y de profundidad uniforme, entonces, a partir de su longitud, anchura y profundidad, se puede determinar fácilmente el volumen de agua que puede contener (para llenarla), el área de la superficie (para cubrirla), y la longitud de su borde (si se requiere saber su medida). Pero si es ovalada con un fondo redondeado, las cantidades anteriores no son sencillas de calcular. Una posibilidad es calcularlas mediante integrales.
Para el cálculo integral de áreas se sigue el siguiente razonamiento:

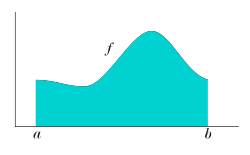
1. Por ejemplo, consideremos la curva mostrada en la figura de arriba, gráfica de la función ${\displaystyle y=f(x)={\sqrt {x}}\,}$, acotada entre ${\displaystyle x=0\,}$ y ${\displaystyle x=1\,}$.
2. La respuesta a la pregunta ¿Cuál es el área bajo la curva de función ${\displaystyle f\,}$, en el intervalo desde ${\displaystyle 0\,}$ hasta ${\displaystyle 1\,}$? es: que el área coincidirá con la integral de ${\displaystyle f\,}$. La notación para esta integral será

${\displaystyle \int _{0}^{1}{\sqrt {x}}\,{\text{d}}x\,\!}$.

Una primera aproximación, aunque no muy precisa, para obtener esta área, consiste en determinar el área del cuadrado unidad cuyo lado lo da la distancia desde x=0 hasta x=1 o también la longitud entre y=f(0)=0 y y=f(1)=1. Su área es exactamente 1x1 = 1. Tal como se puede inferir, el verdadero valor de la integral tendrá que ser más pequeño. Particionando la superficie en estudio, con trazos verticales, de tal manera que vamos obteniendo pequeños rectángulos, y reduciendo cada vez más el ancho de los rectángulos empleados para hacer la aproximación, se obtendrá un mejor resultado. Por ejemplo, dividamos el intervalo en cinco partes, empleando los puntos 0, ¹⁄₅, ²⁄₅,³⁄₅,⁴⁄₅ y finalmente la abscisa 1. Se obtienen cinco rectángulos cuyas alturas se determinan aplicando la función con las abscisas anteriormente descritas (del lado derecho de cada pedazo de la curva), así ${\displaystyle {\sqrt {{}^{1}/_{5}}}}$, ${\displaystyle {\sqrt {{}^{2}/_{5}}}}$, ${\displaystyle {\sqrt {{}^{3}/_{5}}}}$… y así hasta ${\displaystyle {\sqrt {1}}=1\,}$. Sumando las áreas de estos rectángulos, se obtiene una segunda aproximación de la integral que se está buscando,

${\displaystyle {\sqrt {\frac {1}{5}}}\left({\frac {1}{5}}-0\right)+{\sqrt {\frac {2}{5}}}\left({\frac {2}{5}}-{\frac {1}{5}}\right)+\ldots +{\sqrt {\frac {5}{5}}}\left({\frac {5}{5}}-{\frac {4}{5}}\right)\approx 0,7497\,\!}$

Nótese que se está sumando una cantidad finita de valores de la función f, multiplicados por la diferencia entre dos puntos de aproximación sucesivos. Se puede ver fácilmente que las continuas aproximaciones continúan dando un valor más grande que el de la integral. Empleando más pasos se obtiene una aproximación más ajustada, pero no será nunca exacta. Si en vez de 5 subintervalos se toman doce y ahora tomamos las abscisas de la izquierda, tal como se muestra en el dibujo, se obtiene un estimado para el área, de 0,6203, que en este caso es de menor valor que el anteriormente determinado. La idea clave es la transición desde la suma de una cantidad finita de diferencias de puntos de aproximación multiplicados por los respectivos valores de la función, hasta usar pasos infinitamente finos, o infinitesimales. La notación

${\displaystyle \int f(x)\,{\text{d}}x\,\!}$

concibe la integral como una suma ponderada (denotada por la "S" alargada), de los valores de la función multiplicados por pasos de anchura infinitesimal, los llamados diferenciales (indicados por dx).
Con respecto al cálculo real de integrales, el teorema fundamental del cálculo, debido a Newton y Leibniz, es el vínculo fundamental entre las operaciones de derivación e integración. Aplicándolo a la curva raíz cuadrada, se tiene que mirar la función relacionada ${\displaystyle F(x)={\frac {2}{3}}x^{\frac {3}{2}}}$ y simplemente tomar ${\displaystyle F(1)-F(0)\,}$, donde ${\displaystyle 0\,}$ y ${\displaystyle 1\,}$ son las fronteras del intervalo [0,1]. Éste es un ejemplo de una regla general, que dice que para ${\displaystyle f(x)=x^{q}}$, con q ≠ −1, la función relacionada, la llamada primitiva, es ${\displaystyle F(x)={\frac {x^{q+1}}{q+1}}}$. De este modo, el valor exacto del área bajo la curva se calcula formalmente como:

${\displaystyle \int _{0}^{1}{\sqrt {x}}\,dx=\int _{0}^{1}x^{\frac {1}{2}}\,{\text{d}}x=\left.({\frac {2}{3}}x^{\frac {3}{2}})\right|_{0}^{1}={\frac {2}{3}}1^{\frac {3}{2}}-{\frac {2}{3}}0^{\frac {3}{2}}={\frac {2}{3}}.}$

Como se puede ver, la segunda aproximación de 0,7 (con cinco rectangulitos), arrojó un valor superior al valor exacto; en cambio la aproximación con 12 rectangulitos de 0,6203 es una estimación muy por debajo del valor exacto (que es de 0,666...).
Históricamente, después de que los primeros esfuerzos de definir rigurosamente los infinitesimales no fructificasen, Riemann definió formalmente las integrales como el límite de sumas ponderadas, de forma que el dx sugiere el límite de una diferencia (la anchura del intervalo). La dependencia de la definición de Riemann de los intervalos y la continuidad motivó la aparición de nuevas definiciones, especialmente la integral de Lebesgue, que se basa en la habilidad de extender la idea de "medida" de maneras mucho más flexibles. Así, la notación

${\displaystyle \int _{A}f(x)\,{\text{d}}\mu \,\!}$

hace referencia a una suma ponderada de valores en que se divide la función, donde μ mide el peso que se tiene que asignar a cada valor. (Aquí A indica la región de integración.) La geometría diferencial, con su "cálculo de variedades", proporciona otra interpretación a esta notación familiar. Ahora f(x) y dx pasan a ser una forma diferencial, ω = f(x)dx, aparece un nuevo operador diferencial d, conocido como la derivada exterior, y el teorema fundamental pasa a ser el (más general) teorema de Stokes,

${\displaystyle \int _{A}{\mathbf {d}}\omega =\int _{\partial A}\omega ,\,\!}$

a partir del cual se deriva el teorema de Green, el teorema de la divergencia, y el teorema fundamental del cálculo.
Recientemente, los infinitesimales han reaparecido con rigor, a través de innovaciones modernas como el análisis no estándar. Estos métodos no solo reivindican la intuición de los pioneros, también llevan hacia las nuevas matemáticas, y hacen más intuitivo y comprensible el trabajo con cálculo infinitesimal.
A pesar de que hay diferencias entre todas estas concepciones de la integral, hay un solapamiento considerable. Así, el área de la piscina oval se puede hallar como una elipse geométrica, como una suma de infinitesimales, como una integral de Riemann, como una integral de Lebesgue, o como una variedad con una forma diferencial. El resultado obtenido con el cálculo será el mismo en todos los casos.

Definiciones formales[editar]

Hay muchas maneras de definir formalmente una integral, no todas equivalentes. Se establecen diferencias para poder abordar casos especiales que no pueden ser integrables con otras definiciones, pero también en ocasiones por razones pedagógicas. Las definiciones más utilizadas de la integral son las integrales de Riemann y las integrales de Lebesgue.

Integral de Riemann[editar]

Artículo principal: Integral de Riemann

Integral con el planteamiento de Riemann hace una suma basada en una partición etiquetada, con posiciones de muestreo y anchuras irregulares (el máximo en rojo). El verdadero valor es 3,76; la estimación obtenida es 3,648.

La integral de Riemann se define en términos de sumas de Riemann de funciones respecto de particiones etiquetadas de un intervalo. Sea [a,b] un intervalo cerrado de la recta real; entonces una partición etiquetada de [a,b] es una secuencia finita

${\displaystyle a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!}$ y denotamos la partición como ${\displaystyle {\mathit {P}}=\{x_{i}|i=0,1,...,n\}\,\!}$

Convergencia de sumatorios de Riemann a medida en que se parten los intervalos, cuando se muestrea a ■ la derecha, ■ el mínimo, ■ el máximo, o ■ la izquierda.

Esto divide al intervalo [a,b] en n subintervalos [x_i−1, x_i], cada uno de los cuales es "etiquetado" con un punto especificado t_i de; [x_i−1, x_i]. Sea Δ_i = x_i−x_i−1 la anchura del subintervalo i; el paso de esta partición etiquetada es el ancho del subintervalo más grande obtenido por la partición, max_i=1…n Δ_i. Un sumatorio de Riemann de una función f respecto de esta partición etiquetada se define como

${\displaystyle \sum _{i=1}^{n}f(t_{i})\Delta _{i};}$

Así cada término del sumatorio es el área del rectángulo con altura igual al valor de la función en el punto especificado del subintervalo dado, y de la misma anchura que la anchura del subintervalo. La integral de Riemann de una función f sobre el intervalo [a,b] es igual a S si:

Para todo ε > 0 existe δ > 0 tal que, para cualquier partición etiquetada [a,b] con paso más pequeño que δ, se tiene

${\displaystyle \left|S-\sum _{i=1}^{n}f(t_{i})\Delta _{i}\right|<\varepsilon }$, donde ${\displaystyle S=\int _{a}^{b}f=\lim _{\|{\Delta _{i}}\|\to 0}\sum _{i=1}^{n}f(t_{i})\Delta _{i}}$

Cuando las etiquetas escogidas dan el máximo (o mínimo) valor de cada intervalo, el sumatorio de Riemann pasa a ser un sumatorio de Darboux superior (o inferior), lo que sugiere la estrecha conexión que hay entre la integral de Riemann y la integral de Darboux.

Integral de Darboux[editar]

Artículo principal: Integral de Darboux

La Integral de Darboux se define en términos de sumas de los siguientes tipos:

${\displaystyle L({\mathit {f}},P)=\sum _{i}^{n}m_{i}(x_{i}-x_{i-1}),\qquad U({\mathit {f}},P)=\sum _{i}^{n}M_{i}(x_{i}-x_{i-1})}$

Llamadas suma inferior y superior respectivamente, donde:

${\displaystyle M_{i}=\sup\{f(x)|x\in [x_{i-1},x_{i}]\},\qquad m_{i}=\inf\{f(x)|x\in [x_{i-1},x_{i}]\}}$

son las alturas de los rectángulos, y x_i-x_i-1 la longitud de la base de los rectángulos. La integral de Darboux está definida como el único número acotado entre las sumas inferior y superior, es decir,

${\displaystyle L(f,P)\leq \int _{a}^{b}f\leq U(f,P)}$

La interpretación geométrica de la integral de Darboux sería el cálculo del área de la región en [a,b] por el Método exhaustivo. La integral de Darboux de una función f en [a,b] existe si y solo si

${\displaystyle \sup \left\lbrace L(f,P)\right\rbrace =\inf \left\lbrace U(f,P)\right\rbrace }$

Del Teorema de Caracterización que dice que si f es integrable en [a,b] entonces ∀ε>0 ∃ P partición de [a,b] : 0≤U(f,P)-L(f,P)≤ε, evidencia la equivalencia entre las definiciones de Integral de Riemman e Integral de Darboux pues se sigue que^[7]

${\displaystyle \int _{a}^{b}f-\sum _{i=1}^{n}f(t_{i})\Delta _{i}\leq U(f,P)-L(f,P)\leq \varepsilon }$.

Integral de Lebesgue[editar]

Artículo principal: Integral de Lebesgue

Integración de Riemann-Darboux (azul) e integración de Lebesgue (rojo).

La integral de Riemann no está definida para un ancho abanico de funciones y situaciones de importancia práctica (y de interés teórico). Por ejemplo, la integral de Riemann puede integrar fácilmente la densidad para obtener la masa de una viga de acero, pero no se puede adaptar a una bola de acero que se apoya encima. Esto motiva la creación de otras definiciones, bajo las cuales se puede integrar un surtido más amplio de funciones.^[8] La integral de Lebesgue, en particular, logra una gran flexibilidad a base de centrar la atención en los pesos de la suma ponderada.
Así, la definición de la integral de Lebesgue empieza con una medida, μ. En el caso más sencillo, la medida de Lebesgue μ(A) de un intervalo A = [a, b] es su ancho, b − a, así la integral de Lebesgue coincide con la integral de Riemann cuando existen ambas. En casos más complicados, los conjuntos a medir pueden estar altamente fragmentados, sin continuidad y sin ningún parecido a intervalos.
Para explotar esta flexibilidad, la integral de Lebesgue invierte el enfoque de la suma ponderada. Como expresa Folland:^[9] "Para calcular la integral de Riemann de f, se particiona el dominio [a, b] en subintervalos", mientras que en la integral de Lebesgue, "de hecho lo que se está particionando es el recorrido de f".
Un enfoque habitual define primero la integral de la función característica de un conjunto medible A por:

${\displaystyle \int 1_{A}d\mu =\mu (A)}$.

Esto se extiende por linealidad a las funciones escalonadas simples, que solo tienen un número finito n, de valores diferentes no negativos:

${\displaystyle {\begin{aligned}\int s\,d\mu &{}=\int \left(\sum _{i=1}^{n}a_{i}1_{A_{i}}\right)d\mu \\&{}=\sum _{i=1}^{n}a_{i}\int 1_{A_{i}}\,d\mu \\&{}=\sum _{i=1}^{n}a_{i}\,\mu (A_{i})\end{aligned}}}$

(donde la imagen de A_i al aplicarle la función escalonada s es el valor constante a_i). Así, si E es un conjunto medible, se define

${\displaystyle \int _{E}s\,d\mu =\sum _{i=1}^{n}a_{i}\,\mu (A_{i}\cap E).}$

Entonces, para cualquier función medible no negativa f se define

${\displaystyle \int _{E}f\,d\mu =\sup \left\{\int _{E}s\,d\mu \,\colon 0\leq s\leq f{\text{ y }}s{\text{es una funcion escalonada}}\right\};}$

Es decir, se establece que la integral de f es el supremo de todas las integrales de funciones escalonadas que son más pequeñas o iguales que f. Una función medible cualquiera f, se separa entre sus valores positivos y negativos a base de definir

${\displaystyle {\begin{aligned}f^{+}(x)&{}={\begin{cases}f(x),&{\text{si }}f(x)>0\\0,&{\text{de otro modo}}\end{cases}}\\f^{-}(x)&{}={\begin{cases}-f(x),&{\text{si }}f(x)<0\\0,&{\text{de otro modo}}\end{cases}}\end{aligned}}}$

Finalmente, f es Lebesgue integrable si

${\displaystyle \int _{E}|f|\,d\mu <\infty ,\,\!}$

y entonces se define la integral por

${\displaystyle \int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu .\,\!}$

Cuando el espacio métrico en el que están definidas las funciones es también un espacio topológico localmente compacto (como es el caso de los números reales R), las medidas compatibles con la topología en un sentido adecuado (medidas de Radon, de las cuales es un ejemplo la medida de Lebesgue) una integral respecto de ellas se puede definir de otra manera, se empieza a partir de las integrales de las funciones continuas con soporte compacto. De forma más precisa, las funciones compactamente soportadas forman un espacio vectorial que comporta una topología natural, y se puede definir una medida (Radon) como cualquier funcional lineal continuo de este espacio; entonces el valor de una medida en una función compactamente soportada, es también, por definición, la integral de la función. Entonces se continúa expandiendo la medida (la integral) a funciones más generales por continuidad, y se define la medida de un conjunto como la integral de su función característica. Este es el enfoque que toma Bourbaki^[10] y cierto número de otros autores. Para más detalles, véase medidas de Radon.

Otras integrales[editar]

A pesar de que las integrales de Riemann y Lebesgue son las definiciones más importantes de integral, hay unas cuántas más, por ejemplo:

• La integral de Riemann-Stieltjes, una extensión de la integral de Riemann.
• La integral de Lebesgue-Stieltjes, desarrollada por Johann Radon, que generaliza las integrales de Riemann-Stieltjes y de Lebesgue.
• La integral de Daniell, que incluye la integral de Lebesgue y la integral de Lebesgue-Stieltjes sin tener que depender de ninguna medida.
• La integral de Henstock-Kurzweil, definida de forma variada por Arnaud Denjoy, Oskar Perron, y Jaroslav Kurzweil, y desarrollada por Ralph Henstock.
• La integral de Haar, que es la integral de Lebesgue con la medida de Haar.
• La integral de McShane.
• La integral de Bochner.
• La integral de Itō, integral que extiende a la integral de Riemann-Stieltjes, permite integrar respecto a procesos estocásticos que pueden no ser de variación acotada como el movimiento browniano.

Propiedades de la integración[editar]

Linealidad[editar]

• El conjunto de las funciones Riemann integrables en un intervalo cerrado [a, b] forman un espacio vectorial con las operaciones de suma (la función suma de otras dos es la función que a cada punto le hace corresponder la suma de las imágenes de este punto por cada una de las otras dos) y la multiplicación por un escalar. La operación integración

${\displaystyle f\mapsto \int _{a}^{b}f\;dx}$

es un funcional lineal de este espacio vectorial. Así, en primer lugar, el conjunto de funciones integrables es cerrado con la combinación lineal, y en segundo lugar, la integral de una combinación lineal es la combinación lineal de las integrales,

${\displaystyle \int _{a}^{b}(\alpha f+\beta g)(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx.\,}$

• De forma parecida, el conjunto de las funciones reales Lebesgue integrables en un espacio métrico E dado, con la medida μ es cerrado respecto de las combinaciones lineales y por lo tanto forman un espacio vectorial, y la integral de Lebesgue

${\displaystyle f\mapsto \int _{E}fd\mu }$

es un funcional lineal de este espacio vectorial, de forma que

${\displaystyle \int _{E}(\alpha f+\beta g)\,d\mu =\alpha \int _{E}f\,d\mu +\beta \int _{E}g\,d\mu .}$

• De forma más general, si se toma el espacio vectorial de todas las funciones medibles sobre un espacio métrico (E,μ), que toman valores en un espacio vectorial topológico completo localmente compacto V sobre un campo topológico localmente compacto K, f : E → V. Entonces se puede definir una aplicación integración abstracta que a cada función f le asigna un elemento de V o el símbolo ∞,

${\displaystyle f\mapsto \int _{E}fd\mu ,\,}$

que es compatible con las combinaciones lineales. En esta situación, la linealidad se sostiene para el subespacio de las funciones, cuya integral es un elemento de V (es decir, las integrales "finitas"). Los casos más importantes surgen cuando K es R, C, o una extensión finita del campo Qp de números p-ádicos, y V es un espacio vectorial de dimensión finita sobre K, y cuando K=C y V es un espacio de Hilbert complejo.

La linealidad, junto con algunas propiedad naturales de continuidad y la normalización para ciertas clases de funciones "simples", se pueden usar para dar una definición alternativa de integral. Este es el enfoque de Daniell para el caso de funciones reales en un conjunto X, generalizado por Bourbaki a funciones que toman valores en un espacio vectorial topológicamente compacto. Véase Hildebrandt (1953)^[11] para una caracterización axiomática de la integral.

Desigualdades con integrales[editar]

Se verifican varias desigualdades generales para funciones Riemann integrables definidas en un intervalo cerrado y acotado [a, b] y se pueden generalizar a otras nociones de integral (Lebesgue y Daniell).

• Cotas superiores e inferiores. Una función f integrable en [a, b], es necesariamente acotada en el intervalo. Por lo tanto hay dos números reales m y M tales que m ≤ f (x) ≤ M para todo x de [a, b]. Dado que los sumatorios superior e inferior de f sobre [a, b] son también acotados para m(b − a) y M(b − a) respectivamente, de aquí resulta que

${\displaystyle m(b-a)\leq \int _{a}^{b}f(x)\,dx\leq M(b-a).}$

• Desigualdades entre funciones. Si f(x) ≤ g(x) para todo x de [a, b] entonces cada uno de los sumatorios superior e inferior de f son acotados inferior y superiormente por los sumatorios superior e inferior de g respectivamente. Así

${\displaystyle \int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)\,dx.}$

Esto es una generalización de las desigualdades anteriores, dado que M '(b − a) es la integral de la función constante con valor M en el intervalo [a, b].

• Subintervalos. Si [c, d] es un subintervalo de [a, b] y f(x) es no negativa para todo x, entonces

${\displaystyle \int _{c}^{d}f(x)\,dx\leq \int _{a}^{b}f(x)\,dx.}$

• Productos y valores absolutos de funciones. Si f y g son dos funciones, entonces podemos emplear su producto, potencias y valores absolutos:

${\displaystyle (fg)(x)=f(x)g(x),\;f^{2}(x)=(f(x))^{2},\;|f|(x)=|f(x)|.\,}$

Si f es Riemann integrable en [a, b] entonces lo mismo se cumple para |f|, y

${\displaystyle \left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx.}$

Es más, si f y g son ambas Riemann integrables entonces f ², g ², y fg son también Riemann integrables, y

${\displaystyle \left(\int _{a}^{b}(fg)(x)\,dx\right)^{2}\leq \left(\int _{a}^{b}f(x)^{2}\,dx\right)\left(\int _{a}^{b}g(x)^{2}\,dx\right).}$

Esta desigualdad se conoce como desigualdad de Cauchy-Schwarz, y desempeña un papel fundamental en la teoría de los espacios de Hilbert, donde el lado de la derecha se interpreta como el producto escalar de dos funciones integrables f y g en el intervalo [a, b].

• Desigualdad de Hölder. Si p y q son dos números reales, 1 ≤ p, q ≤ ∞ con 1/p + 1/q = 1, y f y g son dos funciones Riemann integrables. Entonces las funciones |f|^p y |g|^q también son integrables y se cumple la desigualdad de Hölder:

${\displaystyle \left|\int f(x)g(x)\,dx\right|\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}\left(\int \left|g(x)\right|^{q}\,dx\right)^{1/q}.}$

Para el caso de p = q = 2, la desigualdad de Hölder pasa a ser la desigualdad de Cauchy–Schwarz.

• Desigualdad de Minkowski. Si p ≥ 1 es un número real y f y g son funciones Riemann integrables. Entonces |f|^p, |g|^p y |f + g|^p son también Riemann integrables y se cumple la desigualdad de Minkowski:

${\displaystyle \left(\int \left|f(x)+g(x)\right|^{p}\,dx\right)^{1/p}\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}+\left(\int \left|g(x)\right|^{p}\,dx\right)^{1/p}.}$

Una desigualdad análoga a ésta para la integral de Lebesgue se usa en la construcción de los espacios L^p.

Convenciones[editar]

En esta sección f es una función real Riemann integrable. La integral

${\displaystyle \int _{a}^{b}f(x)\,dx}$

sobre un intervalo [a, b] está definida si a < b. Esto significa que los sumatorios superiores e inferiores de la función f se evalúan sobre una partición a = x₀ ≤ x₁ ≤ . . . ≤ x_n = b cuyos valores x_i son crecientes. Geométricamente significa que la integración tiene lugar "de izquierda a derecha", evaluando f dentro de intervalos [x_i , x_i +1] donde el intervalo con un índice más grande queda a la derecha del intervalo con un índice más pequeño. Los valores a y b, los puntos extremos del intervalo, se denominan límites de integración de f. Las integrales también se pueden definir si a > b:

• Inversión de los límites de integración. si a > b entonces se define

${\displaystyle \int _{a}^{b}f(x)\,dx=-\int _{b}^{a}f(x)\,dx.}$

Ello, con a = b, implica:

• Integrales sobre intervalos de longitud cero. si a es un número real entonces

${\displaystyle \int _{a}^{a}f(x)\,dx=0.}$

La primera convención es necesaria al calcular integrales sobre subintervalos de [a, b]; la segunda dice que una integral sobre un intervalo degenerado, o un punto, tiene que ser cero. Un motivo para la primera convención es que la integrabilidad de f sobre un intervalo [a, b] implica que f es integrable sobre cualquier subintervalo [c, d], pero en particular las integrales tienen la propiedad de que:

• Aditividad de la integración sobre intervalos. si c es cualquier elemento de [a, b], entonces

${\displaystyle \int _{a}^{b}f(x)\,dx=\int _{a}^{c}f(x)\,dx+\int _{c}^{b}f(x)\,dx.}$

Con la primera convención la relación resultante

${\displaystyle {\begin{aligned}\int _{a}^{c}f(x)\,dx&{}=\int _{a}^{b}f(x)\,dx-\int _{c}^{b}f(x)\,dx\\&{}=\int _{a}^{b}f(x)\,dx+\int _{b}^{c}f(x)\,dx\end{aligned}}}$

queda bien definida para cualquier permutación cíclica de a, b, y c.
En lugar de ver lo anterior como convenciones, también se puede adoptar el punto de vista de que la integración se hace solo sobre variedades orientadas. Si M es una tal forma m-dimensional orientada, y M' es la misma forma con orientación opuesta y ω es una m-forma, entonces se tiene (véase más abajo la integración de formas diferenciales):

${\displaystyle \int _{M}\omega =-\int _{M'}\omega \,.}$

Teorema fundamental del cálculo[editar]

Artículo principal: Teorema fundamental del cálculo

El teorema fundamental del cálculo es la afirmación de que la derivación y la integración son operaciones inversas: si una función continua primero se integra y luego se deriva, se recupera la función original. Una consecuencia importante, en ocasiones denominada el segundo teorema fundamental del cálculo, permite calcular integrales a base de emplear una primitiva de la función a integrar.

Enunciado de los teoremas[editar]

• Teorema fundamental del cálculo. Sea f una función real integrable definida en un intervalo cerrado [a, b]. Si se define F para cada x de [a, b] por

${\displaystyle F(x)=\int _{a}^{x}f(x)\,dx.}$

entonces F es continua en [a, b]. Si f es continua en x de [a, b], entonces F es derivable en x, y F ′(x) = f(x).

• Segundo teorema fundamental del cálculo. Sea f una función real, integrable definida en un intervalo cerrado [a, b]. Si F es una función tal que F ′(x) = f(x) para todo x de [a, b] (es decir, F es una primitiva de f), entonces

${\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a).}$

• Corolario. Si f es una función continua en [a, b], entonces f es integrable en [a, b], y F, definida por

${\displaystyle F(x)=\int _{a}^{b}f(x)\,dx}$

es una primitiva de f en [a, b]. Además,

${\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a).}$

Extensiones[editar]

Integrales impropias[editar]

Artículo principal: Integral impropia

La integral impropia
${\displaystyle \int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi }$
tiene intervalos no acotados tanto en el dominio como en el recorrido.

Una integral de Riemann "propia" supone que el integrando está definido y es finito en un intervalo cerrado y acotado, cuyos extremos son los límites de integración. Una integral impropia aparece cuando una o más de estas condiciones no se satisface. En algunos casos, estas integrales se pueden definir tomando el límite de una sucesión de integrales de Riemann propias sobre intervalos sucesivamente más largos.
Si el intervalo no es acotado, por ejemplo en su extremo superior, entonces la integral impropia es el límite cuando el punto final tiende a infinito.

${\displaystyle \int _{a}^{\infty }f(x)dx=\lim _{b\to \infty }\int _{a}^{b}f(x)dx}$

Si el integrando solo está definido en un intervalo finito semiabierto, por ejemplo (a,b], entonces, otra vez el límite puede suministrar un resultado finito.

${\displaystyle \int _{a}^{b}f(x)dx=\lim _{\epsilon \to 0}\int _{a+\epsilon }^{b}f(x)dx}$

Esto es, la integral impropia es el límite de integrales propias cuando uno de los puntos extremos del intervalo de integración se aproxima, ya sea a un número real especificado, o ∞, o −∞. En casos más complicados, hacen falta límites en los dos puntos extremos o en puntos interiores.
Por ejemplo, la función ${\displaystyle {\tfrac {1}{(x+1){\sqrt {x}}}}}$ integrada desde 0 a ∞ (imagen de la derecha). En el extremo inferior, a medida que x se acerca a 0 la función tiende a ∞, y el extremo superior es él mismo ∞, a pesar de que la función tiende a 0. Así, esta es una integral doblemente impropia. Integrada, por ejemplo, desde 1 hasta 3, con un sumatorio de Riemann es suficiente para obtener un resultado de ${\displaystyle {\tfrac {\pi }{6}}}$. Para integrar desde 1 hasta ∞, un sumatorio de Riemann no es posible. Ahora bien, cualquier límite superior finito, por ejemplo t (con t > 1), da un resultado bien definido, ${\displaystyle {\tfrac {\pi }{2}}-2\arctan {\tfrac {1}{\sqrt {t}}}}$. Este resultado tiene un límite finito cuando t tiende a infinito, que es ${\displaystyle {\tfrac {\pi }{2}}}$. De forma parecida, la integral desde ¹⁄₃ hasta a 1 admite también un sumatorio de Riemann, que por casualidad da de nuevo ${\displaystyle {\tfrac {\pi }{6}}}$. Sustituyendo ¹⁄₃ por un valor positivo arbitrario s (con s < 1) resulta igualmente un resultado definido y da ${\displaystyle -{\tfrac {\pi }{2}}+2\arctan {\tfrac {1}{\sqrt {s}}}}$. Éste, también tiene un límite finito cuando s tiende a cero, que es ${\displaystyle {\tfrac {\pi }{2}}}$. Combinando los límites de los dos fragmentos, el resultado de esta integral impropia es

${\displaystyle {\begin{aligned}\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}&{}=\lim _{s\to 0}\int _{s}^{1}{\frac {dx}{(x+1){\sqrt {x}}}}+\lim _{t\to \infty }\int _{1}^{t}{\frac {dx}{(x+1){\sqrt {x}}}}\\&{}=\lim _{s\to 0}\left(-{\frac {\pi }{2}}+2\arctan {\frac {1}{\sqrt {s}}}\right)+\lim _{t\to \infty }\left({\frac {\pi }{2}}-2\arctan {\frac {1}{\sqrt {t}}}\right)\\&{}={\frac {\pi }{2}}+{\frac {\pi }{2}}\\&{}=\pi .\end{aligned}}}$

Este proceso no tiene el éxito garantizado; un límite puede no existir, o puede ser infinito. Por ejemplo, sobre el intervalo cerrado de 0 a 1 la integral de ${\displaystyle {\tfrac {1}{x^{2}}}}$ no converge; y sobre el intervalo abierto del 1 a ∞ la integral de ${\displaystyle {\tfrac {1}{\sqrt {x}}}}$ no converge.

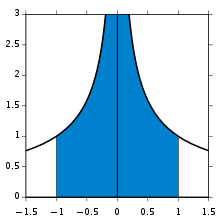
La integral impropia
${\displaystyle \int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}=6}$
no está acotada internamente, pero ambos límites (por la derecha y por la izquierda) existen.

También puede pasar que un integrando no esté acotado en un punto interior, en este caso la integral se ha de partir en este punto, y el límite de las integrales de los dos lados han de existir y han de ser acotados. Así

${\displaystyle {\begin{aligned}\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}&{}=\lim _{s\to 0}\int _{-1}^{-s}{\frac {dx}{\sqrt[{3}]{x^{2}}}}+\lim _{t\to 0}\int _{t}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}\\&{}=\lim _{s\to 0}3(1-{\sqrt[{3}]{s}})+\lim _{t\to 0}3(1-{\sqrt[{3}]{t}})\\&{}=3+3\\&{}=6.\end{aligned}}}$

A la integral similar

${\displaystyle \int _{-1}^{1}{\frac {dx}{x}}\,\!}$

no se le puede asignar un valor de esta forma, dado que las integrales por encima y por debajo de cero no convergen independientemente (en cambio, véase valor principal de Cauchy.)

Integración múltiple[editar]

Artículo principal: Integral múltiple

Integral doble como el volumen limitado por una superficie.

Las integrales se pueden calcular sobre regiones diferentes de los intervalos. En general, una integral sobre un conjunto E de una función f se escribe:

${\displaystyle \int _{E}f(x)\,dx.}$

Aquí x no hace falta que sea necesariamente un número real, sino que puede ser cualquier otra cantidad apropiada, por ejemplo, un vector de R3. El teorema de Fubini demuestra que estas integrales pueden reescribirse como una integral iterada. En otras palabras, la integral se puede calcular a base de integrar las coordenadas una por una.
De la misma manera que la integral definida de una función positiva representa el área de la región encerrada entre la gráfica de la función y el eje x, la integral doble de una función positiva de dos variables representa el volumen de la región comprendida entre la superficie definida por la función y el plano que contiene su dominio. (El mismo volumen puede obtenerse a través de una integral triple — la integral de la función de tres variables — de la función constante f(x, y, z) = 1 sobre la región mencionada antes entre la superficie y el plano, lo mismo se puede hacer con una integral doble para calcular una superficie.) Si el número de variables es mayor, entonces la integral representa un hipervolumen, el volumen de un sólido de más de tres dimensiones que no se puede representar gráficamente.
Por ejemplo, el volumen del paralelepípedo de caras 4 × 6 × 5 se puede obtener de dos maneras:

• Con la integral doble

${\displaystyle \iint _{D}5\ dx\,dy}$

de la función f(x, y) = 5 calculada en la región D del plano xy que es la base del paralelepípedo.

• Con la integral triple

${\displaystyle \iiint _{\mathrm {paralelepipedo} }1\,dx\,dy\,dz}$

de la función constante 1 calculada sobre el mismo paralelepípedo (a pesar de que este segundo método también se puede interpretar como el hipervolumen de un hiperparalelepípedo de cuatro dimensiones que tiene como base el paralelepípedo en cuestión y una altura constante de 1, como la altura es 1 el volumen coincide con el área de la base).

Puesto que es imposible calcular la antiderivada de una función de más de una variable, no existen las integrales múltiples indefinidas: tales integrales son todas definidas.

Integrales de línea[editar]

Artículo principal: Integral de línea

Una integral de línea acumula elementos a lo largo de una curva.

El concepto de integral se puede extender a dominios de integración más generales, tales como las líneas curvas y las superficies. Estas integrales se conocen como integrales de línea e integrales de superficie respectivamente. Tienen importantes aplicaciones en la física cuando se trata con campos vectoriales.
Una integral de línea es una integral donde la función a integrar es evaluada a lo largo de una curva. Se utilizan varias integrales curvilíneas diferentes. En el caso de una curva cerrada también se la denomina integral de contorno.
La función a integrar puede ser un campo escalar o un campo vectorial. El valor de la integral curvilínea es la suma de los valores del campo en los puntos de la línea, ponderados por alguna función escalar de la curva (habitualmente la longitud del arco o, en el caso de un campo vectorial, el producto escalar del campo vectorial por un vector diferencial de la curva). Esta ponderación distingue las integrales curvilíneas de las integrales más sencillas definidas sobre intervalos.
Muchas fórmulas sencillas de la física tienen de forma natural análogas continuas en términos de integrales de línea; por ejemplo, el hecho de que el trabajo sea igual a la fuerza multiplicada por la distancia se puede expresar (en términos de cantidades vectoriales) como:

${\displaystyle W={\vec {F}}\cdot {\vec {d}}}$

que tiene su paralelismo en la integral de línea

${\displaystyle W=\int _{C}{\vec {F}}\cdot d{\vec {s}}}$

que acumula los componentes vectoriales a lo largo de un camino continuo, y así calcula el trabajo realizado por un objeto al moverse a través de un campo, como por ejemplo un campo eléctrico o un campo gravitatorio.

Integrales de superficie[editar]

Artículo principal: Integral de superficie

La definición de las integrales de superficie descansa en la división de la superficie en pequeños elementos de superficie.

Una integral de superficie es una integral definida calculada sobre una superficie (que puede ser un conjunto curvado en el espacio; se puede entender como la integral doble análoga a la integral de línea. La función a integrar puede ser un campo escalar o un campo vectorial. El valor de la integral de superficie es la suma ponderada de los valores del campo en todos los puntos de la superficie. Esto se puede conseguir a base de dividir la superficie en elementos de superficie, los cuales proporcionan la partición para los sumatorios de Riemann.
Como ejemplo de las aplicaciones de las integrales de superficie, se puede considerar un campo vectorial v sobre una superficie S; es decir, para cada punto x de S, v(x) es un vector. Imagínese que se tiene un fluido fluyendo a través de S, de forma que v(x) determina la velocidad del fluido en el punto x. El caudal se define como la cantidad de fluido que fluye a través de S en la unidad de tiempo. Para hallar el caudal, hay que calcular el producto escalar de v por el vector unitario normal a la superficie S en cada punto, lo que nos dará un campo escalar, que integramos sobre la superficie:

${\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }}$.

El caudal de fluido de este ejemplo puede ser de un fluido físico como el agua o el aire, o de un flujo eléctrico o magnético. Así, las integrales de superficie tienen aplicaciones en la física, en particular en la teoría clásica del electromagnetismo.

Integrales de formas diferenciales[editar]

Artículo principal: Forma diferencial

Una forma diferencial es un concepto matemático en los campos del cálculo multivariable, topología diferencial y tensores. La notación moderna de las formas diferenciales, así como la idea de las formas diferenciales como el producto exterior de derivadas exteriores formando un álgebra exterior, fue presentada por Élie Cartan.
Se empieza trabajando en un conjunto abierto de Rⁿ. Una 0-forma se define como una función infinitamente derivable f. Cuando se integra una función f sobre un subespacio de m-dimensional S de Rⁿ, se escribe como

${\displaystyle \int _{S}f\,dx^{1}\cdots dx^{m}.}$

(Los superíndices no son exponentes.) Se puede considerar que dx¹ hasta dxⁿ son objetos formales ellos mismos, más que etiquetas añadidas para hacer que la integral se asemeje a los sumatorios de Riemann. De forma alternativa se pueden ver como covectores, y por lo tanto como una medida de la "densidad" (integrable en un sentido general). A dx¹, …,dxⁿ se las denomina 1-formas básicas.
Se define el conjunto de todos estos productos como las 2-formas básicas, y de forma similar se define el conjunto de los productos de la forma dx^a∧dx^b∧dx^c como las 3-formas básicas. Una k-forma general es por lo tanto una suma ponderada de k-formas básicas, donde los pesos son las funciones infinitamente derivables f. Todas juntas forman un espacio vectorial, siendo las k-formas básicas los vectores base, y las 0-formas (funciones infinitamente derivables) el campo de escalares. El producto exterior se extiende a las k-formas de la forma natural. Sobre Rⁿ como máximo n covectores pueden ser linealmente independientes, y así una k-forma con k > n será siempre cero por la propiedad alternante.
Además del producto exterior, también existe el operador derivada exterior d. Este operador hace corresponder a las k-formas (k+1)-formas. Para una k-forma ω = f dx^a sobre Rⁿ, se define la acción de d por:

${\displaystyle {\mathbf {d}}{\omega }=\sum _{i=1}^{n}{\frac {\partial f}{\partial x_{i}}}dx^{i}\wedge dx^{a}.}$

con extensión a las k-formas generales que se dan linealmente.
Este planteamiento más general permite un enfoque de la integración sobre variedades libre de coordenadas. También permite una generalización natural del teorema fundamental del cálculo, denominada teorema de Stokes, que se puede establecer como

${\displaystyle \int _{\Omega }{\mathbf {d}}\omega =\int _{\partial \Omega }\omega \,\!}$

donde ω es una k-forma general, y ∂Ω indica la frontera de la región Ω. Así en el supuesto de que ω sea una 0-forma y Ω sea un intervalo cerrado de la recta real, el teorema de Stokes se reduce al teorema fundamental del cálculo. En el caso de que ω sea una 1-forma y Ω sea una región de dimensión 2 en el plano, el teorema se reduce al teorema de Green. De manera similar, empleando 2-formas, 3-formas y la dualidad de Hodge, se puede llegar al teorema de Stokes y al teorema de la divergencia. De esta forma puede verse que las formas diferenciales suministran una potente visión unificadora de la integración.

Métodos y aplicaciones[editar]

Cálculo de integrales[editar]

Artículo principal: Métodos de integración

La técnica más básica para calcular integrales de una variable real se basa en el teorema fundamental del cálculo. Se procede de la siguiente forma:

1. Se escoge una función f(x) y un intervalo [a, b].
2. Se halla una antiderivada de f, es decir, una función F tal que F' = f.
3. Se emplea el teorema fundamental del cálculo, suponiendo que ni el integrando ni la integral tienen singularidades en el camino de integración,

   ${\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a).}$

4. Por tanto, el valor de la integral es F(b) − F(a).

Nótese que la integral no es realmente la antiderivada, sino que el teorema fundamental permite emplear las antiderivadas para evaluar las integrales definidas.
A menudo, el paso difícil de este proceso es el de encontrar una primitiva de f. En raras ocasiones es posible echar un vistazo a una función y escribir directamente su primitiva. Muy a menudo, es necesario emplear una de las muchas técnicas que se han desarrollado para evaluar integrales. La mayoría de ellas transforman una integral en otra que se espera que sea más manejable. Entre estas técnicas destacan:

• Integración por cambio de variable
• Integración por partes
• Integración por sustitución trigonométrica
• Integración de fracciones parciales

Incluso si estas técnicas fallan, aún puede ser posible evaluar una integral dada. La siguiente técnica más común es el cálculo del residuo, mientras que la serie de Taylor a veces se puede usar para hallar la primitiva de las integrales no elementales en lo que se conoce como el método de integración por series. También hay muchas formas menos habituales para calcular integrales definidas; por ejemplo, se puede emplear la identidad de Parseval para transformar una integral sobre una región rectangular en una suma infinita. En algunas ocasiones, se puede evaluar una integral empleando un truco; un ejemplo de este tipo se puede ver en la integral de Gauss.
Los cálculos de volúmenes de sólidos de revolución se pueden hacer normalmente con la integración por discos o la integración por capas.
Los resultados específicos que se han encontrado empleando las diferentes técnicas se recogen en la tabla de integrales.

Algoritmos simbólicos[editar]

Artículo principal: Integración simbólica

En muchos problemas de matemáticas, física, e ingeniería en los que participa la integración es deseable tener una fórmula explícita para la integral. Con esta finalidad, a lo largo de los años se han ido publicando extensas tablas de integrales. Con el desarrollo de los ordenadores, muchos profesionales, educadores y estudiantes han recurrido a los sistemas de cálculo algebraico por ordenador, que han sido diseñados específicamente para desarrollar tareas tediosas o difíciles, entre las cuales se encuentra la integración. La integración simbólica presenta un reto especial en el desarrollo de este tipo de sistemas.
Una dificultad matemática importante de la integración simbólica es que, en muchos casos, no existe ninguna fórmula cerrada para la primitiva de una función aparentemente inocente. Por ejemplo, se sabe que las primitivas de las funciones exp (x²), x^x y sen x /x no se pueden expresar con una fórmula cerrada en las que participen solo funciones racionales, exponenciales, logarítmicas, trigonométricas, inversas de las funciones trigonométricas, y las operaciones de suma, multiplicación y composición. En otras palabras, ninguna de estas tres funciones dadas es integrable con funciones elementales. La teoría de Galois diferencial proporciona criterios generales para determinar cuándo la primitiva de una función elemental es a su vez elemental. Por desgracia, resulta que las funciones con expresiones cerradas para sus primitivas son la excepción en vez de ser la regla. En consecuencia, los sistemas de cálculo algebraico por ordenador, no pueden tener la seguridad de poder encontrar una primitiva para una función elemental cualquiera construida de forma aleatoria. En el lado positivo, si se fijan de antemano los "bloques constructivos" de las primitivas, aún es posible decidir si se puede expresar la primitiva de una función dada empleando estos bloques y las operaciones de multiplicación y composición, y hallar la respuesta simbólica en el caso de que exista. El algoritmo de Risch, implementado en Mathematica y en otros sistemas de cálculo algebraico por ordenador, hacen precisamente esto para funciones y primitivas construidas a partir de fracciones racionales, radicales, logaritmos y funciones exponenciales.
Algunos integrandos aparecen con la suficiente frecuencia como para merecer un estudio especial. En particular, puede ser útil tener, en el conjunto de las primitivas, las funciones especiales de la física (como las funciones de Legendre, la función hipergeométrica, la función gamma, etcétera). Es posible extender el algoritmo de Risch-Norman de forma que abarque estas funciones, pero se trata de todo un reto.
La mayoría de los humanos no son capaces de integrar estas fórmulas generales, por lo que en cierto sentido los ordenadores son más hábiles integrando fórmulas muy complicadas. Es poco probable que las fórmulas muy complejas tengan primitivas de forma cerrada, de modo que hasta qué punto esto es una ventaja es una cuestión filosófica abierta a debate.

Cuadratura numérica[editar]

Métodos numéricos de cuadratura: ■ Rectángulo, ■ Trapezoide, ■ Romberg, ■ Gauss.

Artículo principal: Integración numérica

Las integrales que se encuentran en los cursos básicos de cálculo han sido elegidas deliberadamente por su simplicidad, pero las que se encuentran en las aplicaciones reales no siempre son tan asequibles. Algunas integrales no se pueden hallar con exactitud, otras necesitan de funciones especiales que son muy complicadas de calcular, y otras son tan complejas que encontrar la respuesta exacta es demasiado lento. Esto motiva el estudio y la aplicación de métodos numéricos para aproximar integrales. Hoy en día se usan en la aritmética de coma flotante, en ordenadores electrónicos. Para los cálculos a mano surgieron muchas ideas mucho antes; pero la velocidad de los ordenadores de uso general como el ENIAC crearon la necesidad de mejoras.
Los objetivos de la integración numérica son la exactitud, la fiabilidad, la eficiencia y la generalidad. Por ejemplo, la integral

${\displaystyle \int _{-2}^{2}{\tfrac {1}{5}}\left({\tfrac {1}{100}}(322+3x(98+x(37+x)))-24{\frac {x}{1+x^{2}}}\right)dx}$

que tiene el valor aproximado de 6.826 (en la práctica ordinaria no se conoce de antemano la respuesta, por lo que una tarea importante — que no se explora aquí — es decidir en qué momento una aproximación ya es bastante buena.) Un enfoque de "libro de cálculo" divide el intervalo de integración en, por ejemplo, 16 trozos iguales, y calcula los valores de la función.

Valores de la función en los puntos

x	−2,00		−1,50		−1,00		−0,50		0,00		0,50		1,00		1,50		2,00
f(x)	2,22800		2,45663		2,67200		2,32475		0,64400		−0,92575		−0,94000		−0,16963		0,83600
x		−1.75		−1,25		−0,75		−0,25		0,25		0,75		1,25		1.75
f(x)		2,33041		2,58562		2,62934		1,64019		−0,32444		−1,09159		−0,60387		0,31734

Algunas aplicaciones[editar]

Valor medio de una función[editar]

Para calcular el valor medio m de una función f en un intervalo [a,b] se usa la siguiente fórmula:

${\displaystyle m={\frac {1}{b-a}}\int _{a}^{b}f(x)\mathrm {d} x.}$

Nótese que, si la función f es una función escalonada con escalones de igual anchura, esta definición coincide con la media aritmética de los valores de la función. Si los escalones tienen anchuras diferentes, entonces coincide con la media aritmética ponderada donde el valor de la función en cada escalón se pondera con la anchura del escalón. Por lo tanto, esta definición se puede entender como la extensión natural de la media.

Aplicaciones en física[editar]

Muchas leyes de la Física se expresan en forma de ecuaciones diferenciales. En el caso más sencillo, estas ecuaciones diferenciales se resuelven con el cálculo de una primitiva y muchas veces el resultado final que se busca se encuentra con el cálculo de una integral.
Por ejemplo, la integral se aplica para resolver el problema de la caída libre de un cuerpo sometido a la gravedad de la tierra. En la Tierra, la aceleración de la gravedad es aproximadamente g = 9,81 m/s². Por lo tanto un cuerpo que cae libremente empezando su caída con velocidad nula tiene una velocidad que viene dada por la siguiente función:

${\displaystyle v=-g\cdot t}$

El signo negativo es debido a que la gravedad es hacia el centro de la tierra y los sistemas de referencia normalmente se eligen de forma que la dirección positiva es hacia arriba.
Si se quiere saber la distancia que ha recorrido el cuerpo durante un tiempo dado T se puede razonar (empleando análisis no estándar) que en torno a cada instante t la velocidad es constante salvo variaciones infinitesimales, por lo tanto el espacio recorrido en este instante durante un periodo de tiempo infinitesimal dt es v(t)dt, la suma de todos los espacios recorridos durante todos los instantes desde t=0 hasta t=T (el momento en que se quiere saber la distancia recorrida) y se calcula con la integral:

${\displaystyle \ell =\int _{0}^{T}\left(-g\cdot t\;\mathrm {d} t\,\right)}$.

El resultado de esta integral es:

${\displaystyle \ell =\,-({\frac {g}{2}}\cdot T^{2})}$

Otros ejemplos de campos de la física donde se aplican las integrales:

• La energía consumida en un periodo de tiempo es la integral de la potencia durante el tiempo.
• La variación de la carga eléctrica en un condensador durante un periodo de tiempo es la integral de la corriente eléctrica que fluye hacia el condensador durante este tiempo.
• La integración del caudal (metros cúbicos por segundo) que fluye por un conducto proporciona el volumen de fluido que ha pasado por el conducto durante el periodo de integración.

Véase también[editar]

• Tabla de integrales
• Integración numérica
• Derivada
• Signo de Integral
• Portal:Matemática. Contenido relacionado con Matemática.
• Sumatorio
• Límite matemático
• Infinito
• Integral de línea
• Cambio de variable
• Integrales definidas
• Integrales indefinidas

Referencias y notas[editar]

1. Volver arriba ↑ En el caso de las funciones a las que se aplica la definición de Riemann, los resultados coinciden.
2. Volver arriba ↑ Burton, David M. (2005). The History of Mathematics: An Introduction (6ª ed.), McGraw-Hill, p. 359, ISBN 978-0-07-305189-5
3. Volver arriba ↑ Leibniz, Gottfried Wilhelm (1899) (Gerhardt, Karl Immanuel, ed.). Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller, p. 154
4. Volver arriba ↑ Cajori, Florian (1929). A History Of Mathematical Notations, Vol. II, Open Court Publishing, pp. 247–252, ISBN 978-0-486-67766-8
5. Volver arriba ↑ Fourier, Jean Baptiste Joseph (1822). Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231, [1]
6. Volver arriba ↑ W3C (2006). Arabic mathematical notation [2]
7. Volver arriba ↑ Haaser, LaSalle, Sullivan, Norman B.,Joseph P., Joseph A. (1970). Análisis Matemático 1: Curso de Introducción p.546. México,D.F.: Trillas. ISBN 968-24-0132-1. 
8. Volver arriba ↑ Rudin, Walter (1987). "Chapter 1: Abstract Integration", Real and Complex Analysis (International ed.), McGraw-Hill, ISBN 978-0-07-100276-9
9. Volver arriba ↑ Folland, Gerald B. (1984). Real Analysis: Modern Techniques and Their Applications (1ª ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
10. Volver arriba ↑ Bourbaki, Nicolas (2004). Integration I, Springer Verlag, ISBN 3-540-41129-1. En particular, los capítulos III y IV.
11. Volver arriba ↑ Hildebrandt, T. H. (1953). "Integration in abstract spaces", Bulletin of the American Mathematical Society 59(2): 111–139, ISSN 0273-0979 [3]

Bibliografía[editar]

• Apostol, Tom M. (1967). Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd edición). John Wiley & Sons. ISBN 978-0-471-00005-1. 
• Bourbaki, Nicolas (2004). Integration I. Springer. ISBN 3-540-41129-1. . En particular los capítulos III y IV.
• Burton, David M. (2005). The History of Mathematics: An Introduction (6^th edición). McGraw-Hill. p.  359. ISBN 978-0-07-305189-5. 
• Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. pp. 247-252. ISBN 978-0-486-67766-8. 
• Dahlquist, Germund; Björck, Åke (forthcoming). «Chapter 5: Numerical Integration». Numerical Methods in Scientific Computing. Philadelphia: SIAM. 
• Folland, Gerald B. (1984). Real Analysis: Modern Techniques and Their Applications (1st edición). Wiley-Interscience. ISBN 978-0-471-80958-6. 
• Fourier, Jean Baptiste Joseph (1822). Théorie analytique de la chaleur. Chez Firmin Didot, père et fils. p. §231. 
  Disponible en inglés comoFourier, Joseph (1878). The analytical theory of heat. Freeman, Alexander (trans.). Cambridge University Press. pp.  200-201. 
• Heath, T. L., ed. (2002). The Works of Archimedes. Dover. ISBN 978-0-486-42084-4. 
  (Originalmente publicado por Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)
• Hildebrandt, T. H. (1953). «Integration in abstract spaces». Bulletin of the American Mathematical Society 59 (2). pp. 111-139. ISSN 0273-0979. 
• Kahaner, David; Moler, Cleve; Nash, Stephen (1989). «Chapter 5: Numerical Quadrature». Numerical Methods and Software. Prentice-Hall. ISBN 978-0-13-627258-8. 
• Leibniz, Gottfried Wilhelm (1899). Gerhardt, Karl Immanuel, ed. Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band. Berlin: Mayer & Müller. 
• Miller, Jeff. Earliest Uses of Symbols of Calculus. Archivado desde el original el 5 de diciembre de 1998. Consultado el 2 de junio de 2007. 
• O’Connor, J. J.; Robertson, E. F. (1996). A history of the calculus. Consultado el 9 de julio de 2007. 
• Rudin, Walter (1987). «Chapter 1: Abstract Integration». Real and Complex Analysis (International edición). McGraw-Hill. ISBN 978-0-07-100276-9. 
• Saks, Stanisław (1964). Theory of the integral (English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised edición). New York: Dover. 
• Stoer, Josef; Bulirsch, Roland (2002). «Chapter 3: Topics in Integration». Introduction to Numerical Analysis (3rd edición). Springer-Verlag. ISBN 978-0-387-95452-3. .
• W3C (2006). Arabic mathematical notation. 

Libros en internet[editar]

• Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
• Stroyan, K.D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
• Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin, Calculus, Fullerton College, an online textbook
• Garrett, Paul, Notes on First-Year Calculus
• Hussain, Faraz, Understanding Calculus, an online textbook
• Kowalk, W.P., Integration Theory, University of Oldenburg. A new concept to an old problem. Online textbook
• Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
• Numerical Methods of Integration at Holistic Numerical Methods Institute

Enlaces externos[editar]

Wikilibros

• Wikilibros alberga un libro o manual sobre Cálculo. (en inglés)
• La integral definida y la función área, en Descartes.
• The Integrator de Wolfram Research
• Function Calculator de WIMS
• P.S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972) - a cookbook of definite integral techniques
• Definite Integrals
• Web de integrales en español

Obtenido de «https://es.wikipedia.org/w/index.php?title=Integración&oldid=97441003»

Categorías:

• Cálculo integral
• Integrales